2年生 算数「かけ算」導入期の指導で大切にしたいこと（指導案・ワークシートあり）

このブログには国語の実践ばかり掲載していますが、たまには算数の実践も載せます。

2年生算数「かけ算」の実践です。

「かけ算」の導入に当たって大切にしたいことは3つです。

まず、場面のイメージを豊かに経験させること。

子供たちは、「1つ分」がかけられる数、「いくつ分」がかける数と頭で理解していても、1つ分といくつ分を反対に立式してしまうことがあります。

これは言葉のみの浅い理解にとどまり、場面のイメージができていないことが要因です。そこで、

「ケーキが1皿に3個ずつ5皿分あります」

「4人グループの班が6つあります」

など、多様な具体的場面からかけ算の立式をする経験を積むことを大切にします。

 

次に、場面となる対象の中から、「1つ分」と「いくつ分」を自ら設定してかけ算の立式をする場面を設定すること。

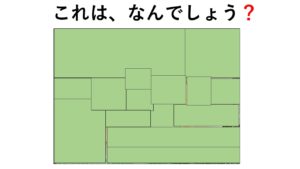
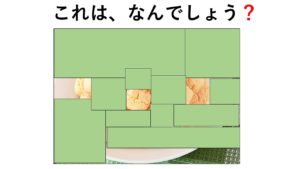
例えば、点字ブロックの●の数え方は、1つ分の設定の仕方によっていろいろな数え方（かけ算の式）ができます。自ら「1つ分」を設定し、その「いくつ分」で考えることは、自己選択、自己決定の力を育てることにもつながります。

 

3つめは、同じ数ずつのいくつ分で立式するよさを実感させること。

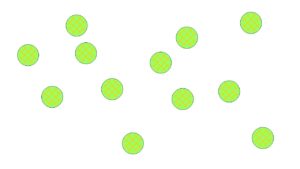
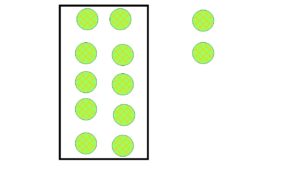
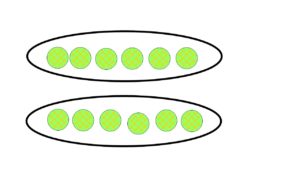
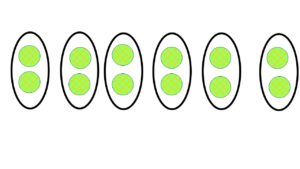
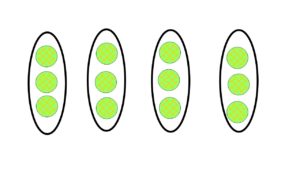
例えば一見不規則に並んだ●の総数を求めるとき、●を規則正しく並べ替えると、かけ算の式で立式することができ、容易に総数を求めることができます。

かけ算を使うことのよさをたくさん実感することが、進んで生活に生かそうとする態度につながると考えます。

 

このようなことを念頭に置き、以下のような具体的な手立てによって授業作りをしました。

①算数的な表現活動
かけ算の意味を理解するために、「具体的場面→半具体物に置き換える→絵や図に表す→言葉に表す→式に表す」という操作・表現の活動を明確にする。そうすることにより、「1つ分の大きさ」と「いくつ分」の理解を深めることができるようにする。また、単元後半の九九を構成する学習では、「九九カルタ」を活用することで、「式→図」の方向でもイメージ化を図る。

②「1つ分」と「いくつ分」を自ら決める場面の設定
導入時での経験をもとにして、子供たちが自由に「1つ分の大きさ」を決めて、その「いくつ分」で全体の数を表す場面を設定する。そうすることで、かけ算の意味理解が深まるとともに、1つの数をほかの数の積としてみる（12＝2×6、6×2、3×4など）ことができるようにする。

③身の回りからかけ算の式で表される場面をさがす活動
身の回りの事物・事象には、かけ算の式で表される場面が数多くある。総和を求めるときにたし算で求めるのは大変であるが、かけ算の式で表し九九を使うことによって効率的に総和を求めることのよさに気づかせる。タブレットを活用し、教室など校舎内でかけ算の式で表されるものを見つけて写真を撮り、共有する活動を設定する。

④「九九カルタ」の活用
かけ算の式に図形のイメージをもたせるために、単元後半の「九九の構成」を「実物大九九カルタ」作りを通して行う。「実物大九九カルタ」とは、九九によってカードの大きさが違うカードのことである。（筑波大学附属小学校の田中博史先生が考案されたもの→「ビジュアル九九カルタ」　今回は教材を買うのではなく、子供たちがカルタを手作りをする。）このカルタを使った数学的活動に楽しみながら取り組むことを通して、かけ算の式と図(形や大きさ)のイメージが結びつくようにする。このカルタを使うことにより、上学年の学習の素地となる経験も積ませることができる。例えば、カルタ遊びをしていると、答えが10になるカルタ（九九）は2×5、5×2の2枚あることや、それらのカルタを重ねてみるとぴったり重なること(乗法の交換法則)に気づく。さらに、4×4や5×5などのカルタは正方形になること(平方数)や、2×5のカルタと3×5のカルタを上下に並べると5×5のカルタと同じ形・大きさになること(結合・分配法則)などを、遊びの中で実感を伴いながら理解させていくことができる。こうしたかけ算の式に付随した図形のイメージは、上学年で新しい問題を解決するときの土台となるイメージとなるはずである。

⑤振り返りの充実
子供たちがかけ算を使うことのよさが感じられるように、毎時間の学習を振り返る活動を大切にする。基本的には毎時間の終末時に、知識を整理したり、見方や考え方のよさを確かめたりする目的で設定する。その際、「どんなことが分かりましたか？」「どのように考えたのがよかったですか？」「どこに目をつけた　のがよかったですか？」「大事なことは何ですか？」等の具体的な発問をするようにする。また、終末時だけでなく、大事にしたい見方・考え方が子供から出たタイミングで、「○○さんが今言った考えはどういうことかな？」「○○さんが言ったことはこういう意味だよね、とペアで再現してみよう」等の発問によって振り返りをさせることも意識する。さらに、終末時に振り返りを書く分量(文字数)の目安として、「５分で５行書く」という目標を例示し、できた子を称賛するなどして書くことへの意欲も高めていく。

「かけ算」第4時の学習指導案例
↓　　↓　　↓

指導案・ワークシート

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

「いっしゅんで消えたのでわかりません」

「では、一度だけ並べ替えるチャンスをあげます！」

 

 

 

 

「これなら、パッと見ただけで分かるよ」

「他の並べ方はないかな？」

 

 

 

 

「いくつありますか？」

「12こです」

「どうして、すぐに分かったの？」

「6このまとまりが、2こだから」

「今のを式になおせますか？」

「6＋6」「6×2」

「ほかの並べ方も考えてみましょう！」

 

 

 

 

「2×6＝12」

 

 

 

 

「3×4＝12」

 

 

 

 

「4×3＝12」

「最初は●がばらばらに並んでいて数えにくかったですが、おしまいにはすぐに何こか分かるようになりましたね。きょうはどのように考えたのがよかったのですか？」

「同じ数ずつ　のまとまりが、いくつ分かを考えると、かけ算の式で表せるので、答えを出しやすい」（まとめ）